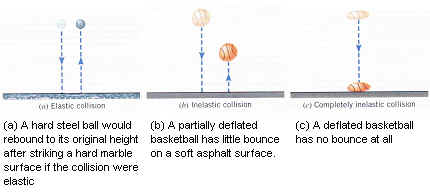
One Dimension Collision (K.E)

    The total linear momentum is conserved when two objects collide, provided that they constitute an isolated system. When the objects are atoms or subatomic particles, the total kinetic energy of the system is often conserved. In other words, the total kinetic energy of the particles before the collision equals to the total kinetic energy of the particles after the collision, so that the kinetic energy gained by one particle is lost by another.

    

   In contrast, when two cars collide, the total kinetic energy after the collison is generally less than that before the collision. Kinetic energy is lost mainly in two ways:

(1) it can be converted into heat because of friction, and
(2) it is spent in creating permanent distortion or damage, as in an automobile collision.
 
Collisions are often classified according to whether the total kinetic energy changes during the collision:
(1) Elastic collison                                (2) Inelastic collision

Example:
As in Fig. A, a ball of mass m1 = 0.250 kg and velocity v01 = +5.00m/s collides head-on with a ball mass m2 = 0.800 kg that is initially at rest. No external force acts on the balls. If the collision is elastic, what are the velocities of the balls after the collision?

 

 

 

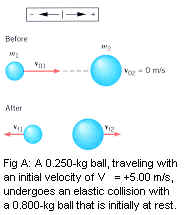
Reasoning: Total linear momentum of the system is conserved. because no external forces act on the system. Momentum conservation applies whether a not the collision is elastic:

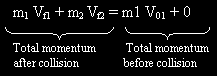
Before and after an elastic collision, the total kinetic energy is the same.

Solution:  The equations above are simultaneous equations containing the two unknown quantities Vf1 and Vf2. To solve them, we begin by rearranging the equation expressing momentum conservation to show that Vf2 = m1(V01 – Vf1)/m2. Substituting this result into the equation expressing the conservation of kinetic energy leads to the following equation for Vf1:

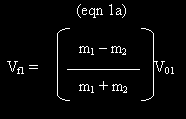
The expression in eqn 1a can be substituted into either of the equations obtained in the Reasoning to show that

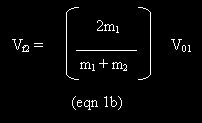
with the given values for m1, m2, and V01, equation 1 yields the following values for Vf1 and Vf2:

            Vf1 = -2.62 m/s                       Vf2 = +2.38 m/s

The negative value for Vf1 indicates that the ball 1 rebound to the left after the collision, while the positive value for Vf2 indicates that ball 2 moves to the right as expected.